Key Points
The last decade has seen considerable advances in statistical, mathematical and computational techniques that are available for the analysis of outbreak data. These advances have greatly increased our capacity to generate meaningful epidemiological information from relatively small numbers of cases of an infection by better representation of the stochastic nature of the outbreak events and improved methods for estimating parameters from such data.
This review focuses on the application of such models, which capture the highly variable dynamics of infection spread amongst small numbers of individuals, in the following areas: quantifying the basic reproduction ratio R0 in the early stages of an outbreak (for foot-and-mouth disease and severe acute respiratory syndrome (SARS)); short-term predictions of outbreak progress (foot-and-mouth disease); trends towards disease emergence or re-emergence (measles in the UK); as an early warning system when there is the threat of a major outbreak (avian influenza); and capturing transmission dynamics within small populations (antibiotic-resistant nosocomial infections).
An important development is the integration of clinical, surveillance and contact-tracing data into the modelling process. This leads to models that are better able to capture the underlying variability in the transmission dynamics and can do so with minimal assumptions. In particular, heterogeneities in the number of secondary infections generated by an infected case (as exemplified by the super-spreaders of the SARS outbreak) mean that contact tracing is essential for a proper quantification of uncertainty in the reproduction ratio.
Advances in the analysis of outbreak data in the near future will probably come from the further development of molecular techniques (to assist contact tracing) and from the better integration of disease data with demographic and environmental information.
Abstract
Recent major disease outbreaks, such as severe acute respiratory syndrome and foot-and-mouth disease in the UK, coupled with fears of emergence of human-to-human transmissible variants of avian influenza, have highlighted the importance of accurate quantification of disease threat when relatively few cases have occurred. Traditional approaches to mathematical modelling of infectious diseases deal most effectively with large outbreaks in large populations. The desire to elucidate the highly variable dynamics of disease spread amongst small numbers of individuals has fuelled the development of models that depend more directly on surveillance and contact-tracing data. This signals a move towards a closer interplay between epidemiological modelling, surveillance and disease-management strategies.
Main
One of the first examples of an epidemiological investigation, as would be recognized today, was the identification by nineteenth-century physician John Snow of the cause of the 1854 London cholera outbreak. By creating a map of cholera deaths and tracing the source of water used by victims, he pinpointed the origin of infection to a contaminated water pump on Broad Street — and in doing so rejected the prevalent 'bad air' theory of cholera transmission1. His approach would not be out of place in modern epidemiology. Recent dramatic disease outbreaks, such as foot-and-mouth disease in the UK, and emerging diseases in the human population, such as severe acute respiratory syndrome (SARS), have highlighted the role of a suite of epidemiological tools — molecular typing, surveillance, tracing of infectious contacts and mathematical modelling — in monitoring disease spread and determining appropriate control measures.
What John Snow lacked in his toolkit was the modern science of mathematical epidemiology, which provides a quantitative framework for describing the spread of disease. In 1911, another physician, Ronald Ross, determined a threshold value for the density of the mosquito vectors, below which the transmission of malaria could not be sustained2. This was an important breakthrough, and heralded the arrival of modern epidemiological theory. This threshold value was given a solid mathematical footing by Kermack and McKendrick3, and arrived, thanks to Macdonald4 and Dietz5, in its modern form as the basic reproduction ratio, R0 (see Ref. 6 for a historical review).
The basic reproduction ratio is the average number of secondary infections produced by one infected individual when that individual is introduced into a previously unexposed population. If R0>1 then, on average, the number of new infections will grow, whereas if R0<1, new infections will, on average, decline and a major outbreak cannot occur.
An extensive and highly successful body of epidemiological theory7 that is centred around this idea lays claim to key concepts, which include outbreak-control strategies, herd immunity8, vaccination and disease eradication policies9 and the identification of 'core' groups in heterogeneous populations as targets for control10. Despite its many successes, it has long been known that this DETERMINISTIC theory, which deals with the average progress of disease spread through a population, does not capture key features of infection dynamics that surround disease invasion, persistence and extinction11,12,13. These elements hinge on chance (STOCHASTIC) events in the chain of transmission, which influence the spread of infection amongst small numbers of individuals14 and can lead to different outbreak scenarios.
Conceptually, probabilistic models that take into account stochastic pathogen dynamics are not new15,16. However, their apparent inscrutability compared with their deterministic counterparts, coupled with the complexities of fitting these models to data to estimate parameters, has limited their widespread use. Recently, however, increasing computational power, modern statistical methods17,18,19,20,21 and availability of detailed outbreak, tracing and surveillance data are allowing the practical implementation of models that better reflect the underlying variability in the biological processes.
This article focuses on recent developments in this area of mathematical modelling with application to specific disease outbreaks. Examples we consider include: (i) quantification of the reproduction ratio in the early stages of an outbreak (for SARS and foot-and-mouth disease); (ii) the distribution of outbreak sizes which allows the monitoring of trends in disease epidemiology towards disease emergence or re-emergence (for measles and avian influenza); and (iii) modelling transmission dynamics within small populations (vancomycin-resistant enterococci in a hospital setting, Escherichia coli O157 on cattle farms and an outbreak of Norovirus in schoolchildren).
SARS, super-spreaders and uncertainty
The global SARS outbreak of 2003 stimulated the development of a range of models from classic deterministic COMPARTMENTAL MODELS22,23 to a detailed stochastic METAPOPULATION MODEL24, all aimed at quantifying the spread of infection and exploring the potential effectiveness of different control measures. The outbreak will be remembered for the dramatic effect of super-spreaders — highly infectious individuals — who seeded several large clusters of cases25.
Quantifying the impact of these individuals on the transmission dynamics was a source of difficulty for the models. The possibility that an infection might generate a super-spreading event introduces inherent uncertainty in predicting the future course of the outbreak. However, it was precisely the heterogeneities in the transmission dynamics of SARS that served to underline the importance of a model structure that captured the possibility of chance or stochastic events in the infection process.
A deterministic model produces a single unique outcome, whereas the probabilistic nature of a stochastic model means that, for the same underlying input parameters, it can produce a tree of possible outcomes. Further variability can arise from various sources, including differences between individuals in risk of acquiring infection26,27,28, infectiousness once infected29 and patterns of contact with other individuals10. Consequently, of two people infected at the Metropole Hotel in Hong Kong, the individual arriving in Vancouver produced no further infections30, whereas the individual arriving in Toronto infected several family members, triggering an outbreak in which ultimately hundreds of people were infected31.
In estimating the EFFECTIVE REPRODUCTION RATIO, R, for the SARS outbreak, Lipsitch et al.32 took a dual approach that spanned both traditional and modern methodologies. The standard deterministic approach is to express R in terms of parameters that describe the average growth rate of infected cases. Here, it is assumed that significant depletion of susceptible individuals has not occurred, so that the number of cases grows exponentially, at a rate determined by R and the GENERATION TIME. Describing the dynamics in this way provides a straightforward estimate for R, with uncertainty in generation-time estimates translating into uncertainty in R. Lipsitch and colleagues32 obtained estimates for R in the range of 2.2–3.6 for generation times ranging from 8 to 12 days.
However, this approach did not capture either the heterogeneities underlying the spread of infection or the variability generated by the stochastic nature of the process. If distributions that capture the heterogeneities are known, simulating the tree of possible outcomes can be relatively straightforward33. The real challenge lies in reversing this process to estimate unknown parameters from an observed rate of spread. The last decade has seen important advances in this area, with increased computing power allowing the practical implementation of likelihood and Bayesian methods18,19,20,34, which explore the tree of possible epidemic paths, and in doing so identify probable ranges for parameter values.
The essence of the Bayesian approach is that it provides a means of incorporating prior knowledge about a system (for example, on the range or probable distribution for a parameter) into subsequent data analysis or model fitting. Lipsitch et al.32 used such a technique to derive estimates for R in the early phase of the SARS outbreak in Hong Kong. Key to their analysis was the availability of detailed clinical and contact-tracing data for the first 205 cases in Singapore. These data enabled them to produce, as input for the model, prior distributions that characterize, without specifying them exactly, the person-to-person variability in infectious period, and the highly skewed distribution of secondary cases produced by an infected individual. The estimates they obtained for R contained considerable uncertainty — a mean of 3.5 with a range of 1.5–7.7 — which reflected the striking heterogeneity in transmission dynamics generated by the super-spreaders. The super-spreaders dramatically increase the variance in the prior distribution for secondary cases, which broadens the spectrum of possible simulated outcomes and consequently increases uncertainty in estimates for R.
The SARS outbreak highlighted the vital role of tracing data in identifying heterogeneities in the number of secondary infections generated by an infected case. In this outbreak, contact tracing was carried out by reconstructing the detailed movements of infected individuals. However, additional means of contact tracing are offered by molecular typing of isolates. RNA viruses, such as the SARS coronavirus, are characterized by high mutation rates, so tracking the evolution of the virus through a population is one method of identifying sources of infection. Whereas molecular typing of isolates was not a practical tool for contact tracing during the SARS outbreak, a microarray has recently been developed for resequencing isolates of the SARS virus35. This type of technical advance might be useful as a practical tool for tracking the spread of pathogens (SARS or other small-genome pathogens) at the individual level in future outbreaks.
Molecular typing could therefore make direct reconstructions of the epidemic tree (of the sort we discuss later for foot-and-mouth disease) a realistic possibility. That said, this form of contact tracing would not replace the tracing of social contacts, as the identification and pre-emptive isolation of potentially infective individuals is, in its own right, an important public-health control measure36,37,38,39,40.
Modelling the UK foot-and-mouth outbreak
The exceptionally close monitoring of the UK foot-and-mouth outbreak in 2001 allowed the development of detailed models that aimed to capture both the temporal and spatial spread of infection41,42,43. These models varied from the MICROSIMULATION MODEL of Keeling et al.42, which was based on known locations of farms, to the more mathematically abstract representation of the spatial clustering of cases adopted by Ferguson et al.41 Although they provide valuable insight into transmission dynamics, the construction of such models often requires simplifying assumptions about important epidemiological processes such as contact structure, infectiousness distribution and susceptibility to infection. Additionally, the models might be difficult to fit to data to obtain estimates for unknown parameters.
If what is required is a retrospective estimate for R, instead of a prediction of the future course of the outbreak41,42, then an alternative is offered by a novel parameter-free method developed by Haydon et al.44 This approach uses the detailed surveillance data to reconstruct the epidemic tree on a case by case basis. This was done by assigning a 'parent' to each 'daughter' case, either from known infectious contacts identified by contact tracing or selected from the premises that were known to have been infectious when the case became infected. This approach is appealing for several reasons: the method is straightforward and transparent; and by using the data directly, it naturally encompasses case-to-case variability (for example, in infectious period), which allows the modelling of a complex spatio-temporal process with minimal assumptions.
Foot-and-mouth disease arose in the UK in early February of 2001, with the first case confirmed on 20 February. A national movement ban was imposed on livestock 3 days later. A retrospective outbreak investigation by the Department for Environment, Food and Rural Affairs (DEFRA, formerly the Ministry for Agriculture Food and Fisheries) estimated that 78 livestock premises across the UK were infected by this time. Prior to the ban, the outbreak was characterized by widespread dissemination of infection on a national scale through animal movements between farms and livestock markets.
Applying the methodology of Haydon et al.44 to the spread of foot-and-mouth prior to the movement ban reveals a highly skewed distribution of secondary cases produced per infected case (Fig. 1). Reconstruction of the outbreak prior to the ban produces an estimate for R0 of 2.99 (95% confidence interval (CI) 1.15–5.23)45, but when infections linked to markets are removed the estimate falls to 1.95 (95% CI 0.95-3.46). This reveals the substantial effect of the markets in disseminating infection. Over a third of infections arising during this period were attributed to markets, indicating that, in the context of foot-and-mouth infection, they were acting as 'super-spreaders'.
Figure 1. Number of secondary cases of foot-and-mouth disease generated prior to the national movement ban (NMB).
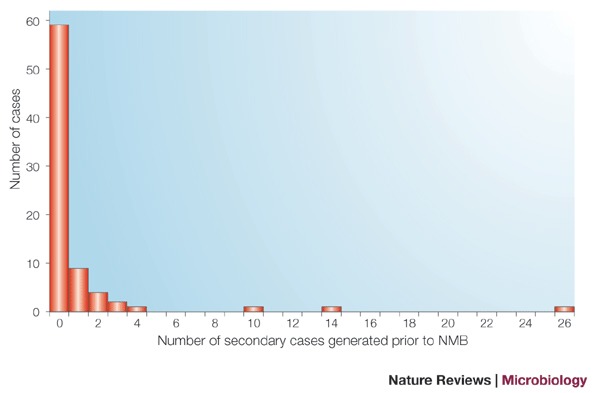
The distribution of the number of secondary cases produced by the 78 cases, which were deemed through subsequent outbreak investigation by the Department for Environment, Food and Rural Affairs to have been infected by the time of imposition of the NMB.
After implementation of the ban, transmission of foot-and-mouth was predominantly local, with estimates for the CASE REPRODUCTION RATIO, Rt, falling shortly after to about 1.5 (Ref. 46). An epidemic is only considered to be under control when the Rt is less than one. The method of Haydon et al.44 was used to monitor the Rt on a week-by-week basis to assess the efficacy of implemented control measures.
Though this approach is ostensibly a means of reconstructing the observed epidemic using tracing data as input, it also provides a flexible environment for examining 'what if' scenarios by 'pruning' branches that depend on the existence of links between particular parents and daughters. This type of analysis indicates that, if the national movement ban had been imposed two days earlier, the final size of the epidemic would have been reduced to 48% (95% CI 39–63%) of its observed size. Output from this model also provides a distribution of Rt values that captures the underlying heterogeneity in the number of secondary cases produced by an infected premises. Coupled with information about the generation time of the pathogen, this can be used to make accurate short-term predictions (Box 1).
The foot-and-mouth and SARS examples highlight the benefits of data-driven approaches in epidemiological modelling. In the case of SARS, the method is parametric: a subset of the data is used to provide prior distributions for relevant parameters, and estimates are obtained by fitting to the total outbreak data. By contrast, the approach for the foot-and-mouth outbreak is non-parametric: distributions are taken directly from the data and used to reconstruct the epidemic tree. In both cases, heterogeneities in the number of secondary infections generated by an infected case (exemplified by the super-spreaders of the SARS outbreak), mean that contact-tracing data is essential for proper quantification of uncertainty in the reproduction ratio.
Assessing the potential threat of avian influenza
Awareness of the potential threat to public health that would be posed by the adaptation of the avian influenza virus to generate a human-to-human transmissible strain has focused attention on surveillance measures to assess whether any such strain has emerged47. The 2003–2004 outbreak of avian influenza in South-East Asia resulted in relatively few human cases, but mortality rates were extremely high — almost 70% of cases were fatal48—a statistic that compares starkly with the 2–3% fatality rate of the Spanish flu pandemic of 1918 (Ref. 49) and the 13% fatality rate of the SARS outbreak37. Therefore, it is vital to identify unusually large clusters of influenza cases as early as possible, as this might signal that a human-to-human transmissible influenza virus has emerged.
Ferguson et al.50 investigated the power of a quantitative approach to detect the occurrence of an unusually large cluster of infection. Owing to the highly stochastic nature of disease transmission among small numbers of individuals, data on a single small cluster of cases is unlikely to be informative, but the distribution of cluster sizes follows a predictable pattern that is dependent on R0 (Refs 51, 52). The method of Ferguson et al.50 is to fit the observed data (excluding the largest cluster to date) to the theoretical distribution. If the largest cluster of avian influenza cases to date is indeed an anomaly, then on fitting of the full data set to the theoretical distribution, this would register as a decrease in goodness-of-fit.
Importantly, the method does not require the largest cluster to have been fully observed — once a certain number of cases has been reached, the goodness-of-fit statistic will drop below a threshold value and trigger public-health alarm bells. Because this technique needs to detect potentially small increases in outbreak sizes, an awareness of the impact of imperfect surveillance is important. In this instance, unbiased under-reporting of cases tends to reduce estimates for R0, but counter-intuitively, under-reporting combined with contact tracing of reported cases can lead to an over-estimate for R0, as small clusters can be disproportionately missed. Nonetheless, this method of estimating R0 can be a useful additional tool as part of an early-warning system that comprises outbreak surveillance, contact tracing to identify cases that cannot be linked to an animal reservoir, and molecular typing to detect the emergence of 'unusual' viral strains. An illustration of these methods, applied to the distribution of outbreak sizes for foot-and-mouth disease in the UK, is given in Box 2.
Re-emergence of measles in the UK?
The distribution of outbreak sizes used by Ferguson et al.50 to describe clusters of avian influenza cases relies on the theory of branching processes53, which describes the patterns of disease extinction and sizes of small outbreaks well when R0 or R are below 1. However, it is only recently that these methods have been used as a surveillance tool to detect unusual patterns and assess trends in underlying epidemiology51,52,54. Specific applications include assessment of the efficacy of vaccination programmes for childhood diseases, in which the aim is to achieve a sufficient level of coverage to maintain R below 1 (Refs 7,9). Using the distribution of small outbreak sizes in vaccinated populations to calculate R can identify potential failures of vaccination control programmes.
Concerns about the potential side effects of the measles, mumps and rubella (MMR) triple vaccine in the UK led to a decline in uptake of the MMR vaccine from 1998 onwards. In parallel, an apparent increase in the frequency and size of measles outbreaks was observed52. By comparing estimates of R for the periods 1995–1998 and 1998–2002, Jansen et al.52 showed that the observed trends reflected a significant increase in R — from 0.47 to 0.82 — which corresponded with the declining levels of immunity. Reassuringly, their upper confidence limits indicate that R is still below the critical value of 1; however, if R rises above 1, the re-emergence of measles as an endemic disease in the UK is possible.
Here, combining statistical analyses of surveillance data with dynamic epidemiological models makes it possible to identify whether trends in the data reflect genuine changes in underlying epidemiology. Moreover, this allows predictions to be made — for example, of probable sizes of clusters should vaccine coverage continue to fall — which, owing to the nonlinear dependence of mean outbreak sizes on R, could not readily be made directly from surveillance data.
Super-spreading of E. coli O157 in cattle
Epidemiological data can be expensive and difficult to collect. In practice, data might be limited to a snapshot of the prevalence of infection in different locations or across multiple populations. However, even in the absence of explicit information on the time-course of infected cases, it is still possible to extract information on the underlying dynamics55,56. This is done by identifying global patterns that the observed data represent. For example, the size of any one measles outbreak is unpredictable, but the distribution of outbreak sizes arising from multiple introductions of infection follows a predictable pattern51,52.
Snapshot data collected from Scottish cattle farms showed that the distribution of cattle shedding the zoonotic pathogen E. coli O157 across farms was highly skewed: at the time of sampling, most farms had no shedding animals, some had intermediate numbers of shedding animals and a small percentage of farms had high numbers of shedding animals. Standard theory7 suggests that, for infections that lead neither to death nor long-term immunity, one would expect an equilibrium prevalence of infection in a population that reflects the balance between transmission and recovery. However, in small groups of animals, stochasticity in the dynamics can prevail, leading both to occasional high prevalences and frequent extinctions of infection from the group.
Globally, we expect to find an equilibrium distribution of prevalences across groups that reflects the balance between introduction of infection (either from an environmental reservoir or from another farm), within-group transmission and stochastic extinction. Matching this theoretical distribution to the observed distribution of prevalences can provide estimates for the within-group R0. Therefore, by examining the global pattern of prevalence, we can draw conclusions about local transmission dynamics. Moreover, investigating departures of the data from the expected distribution can identify important heterogeneities in transmission dynamics.
Closer inspection of the observed prevalences of E. coli O157 and theoretical distributions reveals a discrepancy — the theoretical distribution fails to accurately reproduce the numbers of farms with high numbers of shedding animals. One proposed explanation for this divergence between theory and observation is that the high levels of infection are generated by a small number of cattle that are highly infectious super-spreaders of E. coli O157 (Ref. 56). Incorporating this possibility into the model and estimating the different contributions to R0 made by super-spreading and normal animals indicates that more than 80% of transmission might be derived from fewer than 20% of animals — making these highly infectious individuals obvious targets for control57.
This example shows how snapshot data can shed light on transmission dynamics. By examining infection prevalences in small groups of individuals at different stages in the cycle of invasion, transmission and extinction, it is possible to obtain estimates for relative rates of introduction, transmission and recovery from infection. If data are only available from a single population (see below for the example of a hospital intensive-care unit), a similar approach can be used that captures the processes of invasion, transmission and extinction, but in this case it is necessary to have time-series data on the number of infected cases to quantify the transmission dynamics.
Stochastic dynamics of nosocomial infections
The emergence of antibiotic-resistant nosocomial infections58 has triggered efforts to identify routes of transmission and potential control strategies in the hospital environment. Effective intervention to prevent antibiotic-resistant infections requires an understanding of the most important route of acquisition — whether that is cross-colonization from other patients or de novo acquisition owing to selective pressure of antibiotic use. Surveillance data typically reveal striking variability in the prevalence of infection — for example, 0–80% over several months for vancomycin-resistant enterococci (VRE) in an intensive-care unit in Cook County hospital59. This apparent unpredictability makes it difficult, using standard statistical analyses, to identify routes of colonization unless extensive (and expensive) genotyping information is also obtained.
To analyse data on the prevalence of VRE in an intensive-care unit, an approach conceptually similar to that described above to analyse the E. coli O157 data was used60. A stochastic individual (patient)-based model is used to describe how the distribution of the number of infected patients evolves through time. This model incorporates patient-to-patient transmission of VRE infection, exogenous generation of resistance (equivalent to the infection-introduction term of the E. coli O157 model) and recovery or removal of patients. Parameter estimates are obtained by matching the prevalence data to this distribution at successive observation times using maximum-likelihood methods.
When dealing with small numbers of individuals, such as found in hospital settings, a stochastic model framework is a valuable aid for interpreting outbreak dynamics59,61,62. The power of the distributional approach taken by Pelupessy et al.60 is that it provides a tool for the estimation of key parameters: it allows quantification of the relative importance of cross-colonization and spontaneous acquisition. These analyses showed that cross-colonization is at least as important as a route of transmission as spontaneous acquisition. However, R (given existing control measures such as hand-washing) is approximately 0.7, indicating that cross-colonization alone cannot support endemicity in the unit.
In this instance, extensive genotyping data were available. The consistency revealed by comparing model-based estimates with those obtained directly from the genotyping data highlights this approach (and more recent extensions of the approach to allow for imperfect knowledge of the infection status of patients63) as a valuable epidemiological tool when such data are scarce.
Risk factors for Norovirus infection
It is in the integration of surveillance data with epidemiological modelling that Markov chain Monte Carlo64 (MCMC) methods are especially useful. These are state-of-the-art statistical techniques that have been specifically designed to navigate efficiently through PARAMETER SPACE, assessing the likelihood of different reconstructions of the outbreak and identifying the most probable ranges for parameter values. The key feature of this methodology is the ability to handle distributions in high-dimensional parameter space, allowing both the representation of biologically detailed models and a ready means of handling missing data (which can be represented as unknown parameters). The last decade has seen considerable advances in the application of these methods to epidemiological data17,18,20.
The explicitness with which these methods allow the infection process to be described means that models can better reflect the way the data was generated. This procedure allowed detailed modelling of an outbreak among schoolchildren of Norovirus65, which until recently was generally assumed to be transmitted through the faecal–oral route66,67. However, illness was frequently associated with the onset of projectile vomiting, raising the question of whether these episodes, and subsequent aerosol transmission, increased the risk of infection to other children. Following detailed recording of the outbreak, the model incorporated detailed information for each child, including absences from school, when they reported feeling unwell, when they were exposed in the classroom to other infectious children and when they were exposed to a vomiting episode.
By using MCMC to explore parameter space, the relative risks of infection following different forms of exposure, which optimise the probability of observing the time-course of cases, can be assessed. The estimated parameters showed an increased risk of infection of approximately 20-fold after exposure to vomit, indicating that during these episodes infected children are highly infectious super-spreaders of the virus. In this instance, the result confirms the conclusions of a more standard statistical analysis67. However, in less clear-cut cases, the need to include multiple factors in the model, for example within- and between-class mixing and exposure patterns, a time-varying force-of-infection and differing exposure times of the children, requires the framework of MCMC, which has the flexibility to combine dynamic processes, risk factors and surveillance data.
These methods highlight the way in which current techniques differ from traditional modelling approaches: by combining simulation of the epidemic process with parameter estimation, the models are driven by the data to a greater extent, allowing a more accurate representation of underlying heterogeneities and better estimates of uncertainty in transmission dynamics.
Future directions
In the past few years there have been tremendous advances in statistical, mathematical and computational techniques that are available for analysis of outbreak data. These advances have greatly increased our capacity to generate meaningful epidemiological information from relatively small numbers of cases by better representation of the stochastic nature of outbreak events and improved methods for estimating parameters from such data. The successful application of these techniques depends on the availability of required input data (Fig. 2), which itself has benefited from advances in areas such as rapid diagnosis and strain typing, the design of surveillance systems and information technology.
Figure 2. From surveillance to modelling.
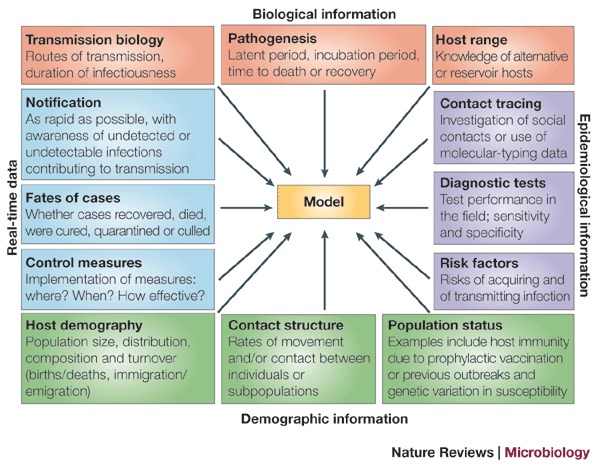
The schematic shown summarizes the inputs required for construction of a useful model.
Several of the examples discussed here (foot-and-mouth disease, measles and SARS) illustrate that the combination of rapid collection and dissemination of clinical and surveillance data with the application of these new analytical approaches can be an invaluable aid to public health or veterinary services that have to make policy decisions in real time. The most obvious contributions are as an early-warning system for situations in which there is potential for a major epidemic, failure of control measures to bring an outbreak under control (Box 1) or trends that increase the likelihood of a major epidemic in the immediate future (Box 2).
Analysis of infectious-disease data will probably advance rapidly in the immediate future by better integration of disease data with demographic and environmental information for the host population. This might include maps of host distributions (in some instances now available at fine scales from census data), information on rates of travel (for example, air traffic between big cities68) or movements of livestock, data on contact patterns for people in cities69, and knowledge of land use and other environmental variables from satellite imagery. Such data will allow more rapid and accurate assessment of probable patterns of spread of an infectious disease from the earliest stages of an outbreak.
Progress in infection modelling should provide considerable benefits for public health and animal health. The rapid detection, identification and assessment of an infectious-disease threat is vital, because the speed with which effective control measures are implemented is usually an important, if not the most important, factor in the size of an outbreak70. Progress in this area requires, as a crucial first step, greater familiarity of public-health and animal-health scientists with mathematical modelling, and a greater familiarity of mathematical modellers with the requirements and expertise of public health and veterinary sciences.
Box 1 | Short-term forecasts in the UK foot-and-mouth outbreak.
By 15 March 2001, 3 weeks after imposition of the movement ban, 280 cases of foot-and-mouth disease had been reported, and subsequent outbreak investigations estimated that 547 livestock premises had been infected. The national movement ban and 'rapid' culling of livestock on infected farms were the only control measures in place on this date, but analysis of the epidemic curve indicates that the outbreak remained out of control. In such cases, accurate short-term predictions of the spread of infection could assist in alerting policy makers to the potential scale of the problem.
Predicting the expected number of case reports requires several inputs: the existing number of infections; the reproduction ratio; the interval between becoming infected and passing on infection to another holding (referred to as the generation time); and the infection-to-reporting interval. Reconstruction of the outbreak using the method of Haydon et al.44 provided arithmetic means and distributions for these parameters for the first 2 weeks of the outbreak following the movement ban.
A stochastic individual (farm)-based model used these distributions to simulate outbreak scenarios from 15 March onwards. Repeated simulations were conducted to produce upper and lower confidence limits on the estimated number of future reports. Our simulated scenarios predicted that the number of reported cases would double within 8–9 days, a forecast that was borne out by subsequent case report data (see Figure).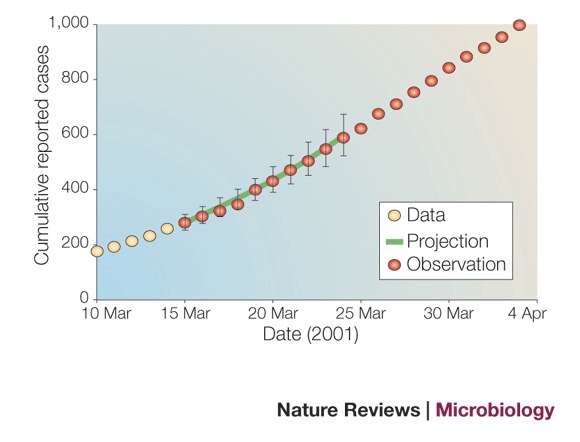
Box 2 | Estimating R for foot-and-mouth outbreaks from 1954 to 1967.
Between 1954 and 1967, 180 typically small foot-and-mouth disease outbreaks were recorded in the UK71. Only 4 generated more than 50 cases — of size 61, 67, 243 and 2,364 — the largest being the well-known epidemic of 1967–1968.
We illustrate the approach of Ferguson et al.50 by using it to determine the effective reproduction ratio, R, for these outbreaks and assess whether the 1967–1968 epidemic was unusually large or within probable ranges given our estimate for R. The probability (P(n)) for the number of cases (n) generated in an outbreak with R<1 is given by51,52:
Excluding the largest outbreak (of 2,364 cases) and fitting this distribution to the remaining 179 outbreaks provides an estimate for R of 0.83 (95% confidence interval (CI) 0.75–0.9) and an acceptable fit (P>0.3, evaluated by simulation following Ferguson et al.50) to the data (see Figure part a, which shows the observed and theoretical distribution of numbers of secondary cases for 179 outbreaks of foot-and-mouth disease arising between 1954 and 1966). Comparison with the full data set of 180 outbreaks reveals a highly significant reduction in goodness-of-fit (P<0.0001), indicating that the 1967–1968 outbreak was unusually large given prior estimates for R.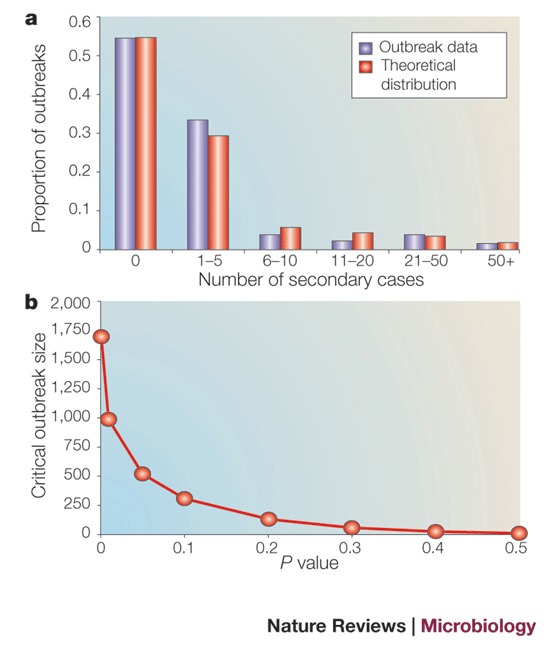
The point at which the goodness-of-fit statistic reaches a critical value determines a crucial size above which an outbreak can be regarded as epidemiologically distinct from preceding ones. Part b of the figure shows how the critical outbreak size depends on the level of confidence required in this assessment (quantified by the P value). Here, to be 95% confident that the largest outbreak in question is unusually large, its size should exceed approximately 500. An outbreak below this threshold, though constituting an important incident for the livestock industry, should not automatically be regarded as a failure of implemented control policies.
More detailed analyses of the 1967–1968 outbreak have confirmed that it was indeed epidemiologically distinct from previous outbreaks; in particular, it was characterized by unusual atmospheric conditions that led to high levels of wind-borne virus transmission in the early stages72. This resulted in high values for R that subsequently fell to about 2.0 (Ref. 73) — a value significantly higher than our estimate for the preceding 179 outbreaks.
Acknowledgements
The authors gratefully acknowledge the support of the Wellcome Trust through the International Partnership Research Award in Veterinary Epidemiology consortium, the support of the Department for Environment, Food and Rural Affairs through the Veterinary Research Training Initiative and a Mathematical Biology Research Training Fellowship to L.M. The authors also thank M. Chase-Topping and S. St Rose for their valuable contributions to the work described here.
Glossary
- DETERMINISTIC
A process that does not contain an element of chance. Deterministic models are often used to describe the progress of an epidemic through large populations, in which small fluctuations at the individual level are assumed not to have an important effect on the dynamics.
- STOCHASTIC
A process that incorporates an element of chance; every realization of the process can produce a different outcome. Stochastic effects are particularly important when the numbers involved are small, for example, at the start of, or during, the 'tail' of an epidemic, when there are few infectious individuals.
- COMPARTMENTAL MODEL
A model in which discrete subsets of the host population are defined according to their infection status. Commonly used compartments are susceptible, latent infected, infectious and recovered or removed.
- METAPOPULATION MODEL
A model comprising a set of epidemiologically linked subpopulations.
- EFFECTIVE REPRODUCTION RATIO
The average number of secondary infections that is produced by one infected individual when that individual is introduced into a population that might have been previously exposed to infection, contain vaccinated individuals or be subject to control measures to limit transmission.
- GENERATION TIME
The mean time interval between an individual becoming infected and an individual that they infect becoming infected.
- MICROSIMULATION MODEL
A stochastic model in which each individual in the population is represented explicitly, as opposed to tracking the number of individuals in each of a set of compartments.
- CASE REPRODUCTION RATIO
The average number of secondary infections that is produced by a single individual infected at time t. It is typically smaller than the basic reproduction ratio, as factors such as depletion of susceptible individuals or implementation of control measures will reduce the number of secondary cases generated.
- PARAMETER SPACE
The range of biologically plausible values that can be taken by the parameters of a model.
Biographies
Louise Matthews has worked as a post-doctoral researcher, and currently as a research fellow, at the University of Edinburgh since 1997. Her research interests lie in the application of mathematical models to infectious-disease data to investigate within-host dynamics of disease pathogenesis, metapopulation dynamics and persistence of rare pathogens, control strategies and their optimal implementation, and identification of heterogeneities such as super-spreaders, which drive the spread of disease.
Mark Woolhouse has held the chair of Veterinary Public Health and Quantitative Epidemiology at the University of Edinburgh since 1997. His research interests concern the epidemiology and pathogenesis of animal and human infectious diseases. He works on a variety of infectious disease systems, ranging from prion diseases to viruses, bacteria, protozoa and helminths. The common theme is the development of a formal, quantitative understanding of the dynamics of parasites and pathogens within their host populations, with particular emphasis on informing the design of disease control programmes.
Related links
DATABASES
Entrez
CDC Infectious disease information
Competing interests
The authors declare no competing financial interests.
References
- 1.Vinten-Johansen P, Brody H, Paneth N, Rachman S, Rip M. Cholera, Chloroform and the Science of Medicine; A Life of John Snow. 2003. [Google Scholar]
- 2.Ross R. The Prevention of Malaria. 1911. [Google Scholar]
- 3.Kermack WO, McKendrick AG. Contributions to the mathematical theory of epidemics — I. 1927. Bull. Math. Biol. 1991;53:33–55. doi: 10.1007/BF02464423. [DOI] [PubMed] [Google Scholar]
- 4.Macdonald G. The analysis of equilibrium in malaria. Trop. Dis. Bull. 1952;49:813–829. [PubMed] [Google Scholar]
- 5.Dietz K. Epidemiology. 1975. pp. 104–121. [Google Scholar]
- 6.Heesterbeek JAP. A brief history of R0 and a recipe for its calculation. Acta Biotheor. 2002;50:189–204. doi: 10.1023/A:1016599411804. [DOI] [PubMed] [Google Scholar]
- 7.Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. 1991. [Google Scholar]
- 8.Fine PEM. Herd immunity: history, theory, practice. Epidemiol. Rev. 1993;15:265–302. doi: 10.1093/oxfordjournals.epirev.a036121. [DOI] [PubMed] [Google Scholar]
- 9.Gay NJ. The theory of measles elimination: implications for the design of elimination strategies. J. Infect. Dis. 2004;189:S27–S35. doi: 10.1086/381592. [DOI] [PubMed] [Google Scholar]
- 10.Yorke JA, Hethcote HW, Nold A. Dynamics and control of transmission of gonorrhea. Sex. Transm. Dis. 1978;5:51–56. doi: 10.1097/00007435-197804000-00003. [DOI] [PubMed] [Google Scholar]
- 11.Bartlett MS. The critical community size for measles in the United States. J. R. Stat. Soc. Ser. A. 1960;123:37–44. doi: 10.2307/2343186. [DOI] [Google Scholar]
- 12.Keeling MJ. Modelling the persistence of measles. Trends Microbiol. 1997;5:513–518. doi: 10.1016/S0966-842X(97)01147-5. [DOI] [PubMed] [Google Scholar]
- 13.Swinton J, Harwood J, Grenfell BT, Gilligan CA. Persistence thresholds for phocine distemper virus infection in harbour seal Phoca vitulina metapopulations. J. Anim. Ecol. 1998;67:54–68. doi: 10.1046/j.1365-2656.1998.00176.x. [DOI] [Google Scholar]
- 14.Becker NG. Analysis of Infectious Disease Data. 1989. [Google Scholar]
- 15.Bailey NTJ. The Mathematical Theory of Infectious Diseases and its Applications. 1975. [Google Scholar]
- 16.Bartlett MS. Stochastic Population Models in Ecology and Epidemiology. 1960. [Google Scholar]
- 17.Cauchemez S, Carrat F, Viboud C, Valleron AJ, Boelle PY. A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data. Stat. Med. 2004;23:3469–3487. doi: 10.1002/sim.1912. [DOI] [PubMed] [Google Scholar]
- 18.Gibson GJ. Markov chain Monte Carlo methods for fitting spatiotemporal stochastic models in plant epidemiology. J. R. Stat. Soc. Ser. C. 1997;46:215–233. doi: 10.1111/1467-9876.00061. [DOI] [Google Scholar]
- 19.Gibson GJ, Kleczkowski A, Gilligan CA. Bayesian analysis of botanical epidemics using stochastic compartmental models. Proc. Natl Acad. Sci. USA. 2004;101:12120–12124. doi: 10.1073/pnas.0400829101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.O'Neill PD, Balding DJ, Becker NG, Eerola M, Mollison D. Analyses of infectious disease data from household outbreaks by Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. C. 2000;49:517–542. doi: 10.1111/1467-9876.00210. [DOI] [Google Scholar]
- 21.O'Neill PD. A tutorial introduction to Bayesian inference for stochastic epidemic models using Markov chain Monte Carlo methods. Math. Biosci. 2002;180:103–114. doi: 10.1016/S0025-5564(02)00109-8. [DOI] [PubMed] [Google Scholar]
- 22.Chowell G, Fenimore PW, Castillo-Garsow MA, Castillo-Chavez C. SARS outbreaks in Ontario, Hong Kong and Singapore: the role of diagnosis and isolation as a control mechanism. J. Theor. Biol. 2003;224:1–8. doi: 10.1016/S0022-5193(03)00228-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang WD, Ruan SG. Simulating the SARS outbreak in Beijing with limited data. J. Theor. Biol. 2004;227:369–379. doi: 10.1016/j.jtbi.2003.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Riley S, et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science. 2003;300:1961–1966. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- 25.Li YG, et al. Predicting super spreading events during the 2003 severe acute respiratory syndrome epidemics in Hong Kong and Singapore. Am. J. Epidemiol. 2004;160:719–728. doi: 10.1093/aje/kwh273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Boelle PY, Cesbron JY, Valleron AJ. Epidemiological evidence of higher susceptibility to vCJD in the young. BMC Infect. Dis. 2004;4:26. doi: 10.1186/1471-2334-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hunter N. PrP genetics in sheep and the implications for scrapie and BSE. Trends Microbiol. 1997;5:331–334. doi: 10.1016/S0966-842X(97)01081-0. [DOI] [PubMed] [Google Scholar]
- 28.Woolhouse MEJ, Etard JF, Dietz K, Ndhlovu PD, Chandiwana SK. Heterogeneities in schistosome transmission dynamics and control. Parasitology. 1998;117:475–482. doi: 10.1017/S003118209800331X. [DOI] [PubMed] [Google Scholar]
- 29.Donaldson AI, Alexandersen S, Sorensen JH, Mikkelsen T. Relative risks of the uncontrollable (airborne) spread of FMD by different species. Vet. Rec. 2001;148:602–604. doi: 10.1136/vr.148.19.602. [DOI] [PubMed] [Google Scholar]
- 30.Health Canada [online] <www.hc-sc.gc.ca/english/protection/warnings/sars/learning/EngSe30_ch2.htm> (2004).
- 31.Svoboda T, et al. Public health measures to control the spread of the severe acute respiratory syndrome during the outbreak in Toronto. N. Engl. J. Med. 2004;350:2352–2361. doi: 10.1056/NEJMoa032111. [DOI] [PubMed] [Google Scholar]
- 32.Lipsitch M, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300:1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Renshaw E. Modelling Biological Populations in Space and Time. 1993. [Google Scholar]
- 34.Gibson GJ, Renshaw E. Likelihood estimation for stochastic compartmental models using Markov chain methods. Statistics and Computing. 2001;11:347–358. doi: 10.1023/A:1011973120681. [DOI] [Google Scholar]
- 35.Wong CW, et al. Tracking the evolution of the SARS coronavirus using high-throughput, high-density resequencing arrays. Genome Res. 2004;14:398–405. doi: 10.1101/gr.2141004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Anderson RM, et al. Epidemiology, transmission dynamics and control of SARS: the 2002–2003 epidemic. Philos. Trans. R. Soc. Lond. B. 2004;359:1091–1105. doi: 10.1098/rstb.2004.1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Donnelly CA, et al. Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong. Lancet. 2003;361:1761–1766. doi: 10.1016/S0140-6736(03)13410-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Eames KTD, Keeling MJ. Contact tracing and disease control. Proc. R. Soc. Lond. B. 2003;270:2565–2571. doi: 10.1098/rspb.2003.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.FitzGerald MR, Thirlby D, Bedford CA. The outcome of contact tracing for gonorrhoea in the United Kingdom. Int. J. STD AIDS. 1998;9:657–660. doi: 10.1258/0956462981921305. [DOI] [PubMed] [Google Scholar]
- 40.Fraser C, Riley S, Anderson RM, Ferguson NM. Factors that make an infectious disease outbreak controllable. Proc. Natl Acad. Sci. USA. 2004;101:6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ferguson NM, Donnelly CA, Anderson RM. The foot-and-mouth epidemic in Great Britain: pattern of spread and impact of interventions. Science. 2001;292:1155–1160. doi: 10.1126/science.1061020. [DOI] [PubMed] [Google Scholar]
- 42.Keeling MJ, et al. Dynamics of the 2001 UK foot and mouth epidemic: stochastic dispersal in a heterogeneous landscape. Science. 2001;294:813–817. doi: 10.1126/science.1065973. [DOI] [PubMed] [Google Scholar]
- 43.Morris RS, Wilesmith JW, Stern MW, Sanson RL, Stevenson MA. Predictive spatial modelling of alternative control strategies for the foot-and-mouth disease epidemic in Great Britain, 2001. Vet. Rec. 2001;149:137–144. doi: 10.1136/vr.149.5.137. [DOI] [PubMed] [Google Scholar]
- 44.Haydon DT, et al. The construction and analysis of epidemic trees with reference to the 2001 UK foot-and-mouth outbreak. Proc. R. Soc. Lond. B. 2003;270:121–127. doi: 10.1098/rspb.2002.2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Woolhouse MEJ, Shaw DJ, Matthews L, Chase-Topping M, St Rose S. Proceedings of the 6th International Congress of Veterinary Virology. 2003. Epidemiology and control of foot-and-mouth disease in the UK. [Google Scholar]
- 46.Woolhouse MEJ, et al. Epidemiology. Foot-and-mouth disease under control in the UK. Nature. 2001;411:258–259. doi: 10.1038/35077149. [DOI] [PubMed] [Google Scholar]
- 47.WHO Estimating the impact of the next influenza pandemic: enhancing preparedness [online] <www.who.int/csr/disease/influenza/preparedness2004_12_08/en/> (2004).
- 48.Trampuz A, Prabhu RM, Smith TF, Baddour LM. Avian influenza: a new pandemic threat? Mayo Clin. Proc. 2004;79:523–530. doi: 10.4065/79.4.523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Taubenberger JK, Reid AH, Krafft AE, Bijwaard KE, Fanning TG. Initial genetic characterization of the 1918 “Spanish” influenza virus. Science. 1997;275:1793–1796. doi: 10.1126/science.275.5307.1793. [DOI] [PubMed] [Google Scholar]
- 50.Ferguson NM, Fraser C, Donnelly CA, Ghani AC, Anderson RM. Public health risk from the avian H5N1 influenza epidemic. Science. 2004;304:968–969. doi: 10.1126/science.1096898. [DOI] [PubMed] [Google Scholar]
- 51.Farrington CP, Kanaan MN, Gay NJ. Branching process models for surveillance of infectious diseases controlled by mass vaccination. Biostatistics. 2003;4:279–295. doi: 10.1093/biostatistics/4.2.279. [DOI] [PubMed] [Google Scholar]
- 52.Jansen VA, et al. Measles outbreaks in a population with declining vaccine uptake. Science. 2003;301:804. doi: 10.1126/science.1086726. [DOI] [PubMed] [Google Scholar]
- 53.Cox DR, Miller HD. The Theory of Stochastic Processes. 1997. [Google Scholar]
- 54.De Serres G, Gay NJ, Farrington CP. Epidemiology of transmissible diseases after elimination. Am. J. Epidemiol. 2000;151:1039–1048. doi: 10.1093/oxfordjournals.aje.a010145. [DOI] [PubMed] [Google Scholar]
- 55.Keeling MJ, Brooks SP, Gilligan CA. Using conservation of pattern to estimate spatial parameters from a single snapshot. Proc. Natl Acad. Sci. USA. 2004;101:9155–9160. doi: 10.1073/pnas.0400335101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Matthews, L. et al. Super-shedding cattle and the transmission dynamics of Escherichia coli O157. Epidemiol. Infect. (in the press). Uses distribution of prevalences across cattle populations to quantify within-herd transmission dynamics and identify important heterogeneities in the transmission dynamics. [DOI] [PMC free article] [PubMed]
- 57.Woolhouse MEJ, et al. Heterogeneities in the transmission of infectious agents: implications for the design of control programs. Proc. Natl Acad. Sci. USA. 1997;94:338–342. doi: 10.1073/pnas.94.1.338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cohen ML. Epidemiology of drug resistance — implications for a post-antimicrobial era. Science. 1992;257:1050–1055. doi: 10.1126/science.257.5073.1050. [DOI] [PubMed] [Google Scholar]
- 59.Austin DJ, Bonten MJM, Weinstein RA, Slaughter S, Anderson RM. Vancomycin-resistant enterococci in intensive-care hospital settings: transmission dynamics, persistence, and the impact of infection control programs. Proc. Natl Acad. Sci. USA. 1999;96:6908–6913. doi: 10.1073/pnas.96.12.6908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pelupessy I, Bonten MJM, Diekmann O. How to assess the relative importance of different colonization routes of pathogens within hospital settings. Proc. Natl Acad. Sci. USA. 2002;99:5601–5605. doi: 10.1073/pnas.082412899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Cooper BS, Medley GF, Scott GM. Preliminary analysis of the transmission dynamics of nosocomial infections: stochastic and management effects. J. Hosp. Infect. 1999;43:131–147. doi: 10.1053/jhin.1998.0647. [DOI] [PubMed] [Google Scholar]
- 62.Sebille V, Valleron AJ. A computer simulation model for the spread of nosocomial infections caused by multidrug-resistant pathogens. Comput. Biomed. Res. 1997;30:307–322. doi: 10.1006/cbmr.1997.1451. [DOI] [PubMed] [Google Scholar]
- 63.Cooper B, Lipsitch M. The analysis of hospital infection data using hidden Markov models. Biostatistics. 2004;5:223–237. doi: 10.1093/biostatistics/5.2.223. [DOI] [PubMed] [Google Scholar]
- 64.Gamerman D. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. 1997. [Google Scholar]
- 65.O'Neill, P. D. & Marks, P. J. Bayesian model choice and infection route modelling in an outbreak of Norovirus. Stat. Med. 7 Apr. 2005 [epub ahead of print]. Uses MCMC to model and determine risk factors for the acquisition of Norovirus infection in schoolchildren. [DOI] [PubMed]
- 66.Marks PJ, et al. Evidence for airborne transmission of Norwalk-like virus (NLV) in a hotel restaurant. Epidemiol. Infect. 2000;124:481–487. doi: 10.1017/S0950268899003805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Marks PJ, et al. A school outbreak of Norwalk-like virus: evidence for airborne transmission. Epidemiol. Infect. 2003;131:727–736. doi: 10.1017/S0950268803008689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hufnagel L, Brockmann D, Geisel T. Forecast and control of epidemics in a globalized world. Proc. Natl Acad. Sci. USA. 2004;101:15124–15129. doi: 10.1073/pnas.0308344101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Eubank S, et al. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- 70.Woolhouse, M. E. J., Haydon, D. T. & Antia, R. Emerging pathogens: the epidemiology and evolution of species jumps. Trends Ecol. Evol. (in the press). [DOI] [PMC free article] [PubMed]
- 71.Northumberland Report: Report of the Committee of Inquiry on Foot-and–Mouth Disease (Her Majesty's Stationary Office, London, 1969).
- 72.Tinline R. Lee wave hypothesis for initial pattern of spread during 1967–68 foot and mouth epizootic. Nature. 1970;227:860–862. doi: 10.1038/227860b0. [DOI] [PubMed] [Google Scholar]
- 73.Haydon DT, Woolhouse MEJ, Kitching RP. An analysis of foot-and-mouth–disease epidemics in the UK. IMA J. Math. Appl. Med. Biol. 1997;14:1–9. doi: 10.1093/imammb/14.1.1. [DOI] [PubMed] [Google Scholar]


